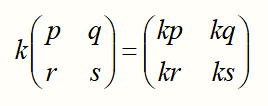natinedJs ⓚ 2023 Matriks pertama kali diperkenalkan oleh Athur Cayley pada tahun 1859 di Inggris. Matriks diperkenalkan dalam studi sistem persamaan linear dan transformasi linear. Awalnya matriks hanya dianggap permainan karna tidak bisa diaplikasikan oleh beberapa matematikawan dan juga orang-orang yang menggeluti matematika. Pada akhirnya tahun 1925 tepatnya setelah 30 tahun Arthur Cayley meninggal, matriks digunakan pada mekanika kuantum. Selanjutnya matriks mengalami perkembangan yang pesat dan digunakan dalam berbagai bidang.
Penemu Matriks :
- Matriks adalah suatu susunan bilangan atau huruf berbentuk segi empat yang diatur dalam baris dan kolom dan dibatasi oleh dua kurung. Unsur-unsur tersebut bisa berupa bilangan dan juga suatu peubah.
- Nama matriks menggunakan huruf besar seperti A, B, C dst. Sedangkan anggota (elemen) dari matriks yang berupa huruf dituliskan menggunakan huruf kecil.
- Tanda yang digunakan adalah kurung biasa “( )” atau kurung siku “ [ ]”
Notasi :
atau dapat di tulis dengan A=aij dengan i = baris (1,2,....m) dan j= kolom (1,2,...,n)
Contoh :
Matriks di atas adalah Matriks A dengan a13 = "elemen baris ke 1 kolom ke tiga"adalah 2, a22 = 4, a32 = 5, dst.
ORDO MATRIKS
matriks memiliki ukuran yang disebut dengan ordo, yang ditulis dengan aturan "Baris x Kolom"
contoh :
Matriks A2x2 merupakan matriks berukuran 2 baris dan 2 kolom.
Matriks A2x2 merupakan matriks berukuran 2 baris dan 2 kolom.
Matriks B2x3 merupakan matriks berukuran 2 baris dan 3 kolom.
Matriks C3x3 merupakan matriks berukuran 3 baris dan 3 kolom.
Sehingga untuk matriks A di bawah ini beukuran mxn atau dapat ditulis Amxn
OPERASI PADA MATRIKS
a. Kesamaan matriks
Definisi:
Dua matriks didefinisikan sama jika keduanya mempunyai ukuran atau dimensi yang sama dan elemen-elemen yang berpadanan sama.
Dalam notasi matriks:
jika A = (aij) dan B = (bij) mempunyai ukuran yang sama maka A=B jika dan hanya jika(aij)=(bij), atau secara ekuivalen aij=bij, untuk semua i dan j.
Contoh :
maka A = Balasannya :
maka A = B
a11 = b11 = 1
a12 = b12 = 2
a21 = b21 = 1
a22 = b22 = 3
b. Penjumlahan dan pengurangan matriks
Dua buah matriks dapat dijumlahkan dan dikurangkan apabila memiliki Ordo yang sama (ukurannya sama) .
Cara :
> Matriks A + B adalah matriks yang diperoleh dengan menambahkan elemen-elemen A dengan elemen-elemen B yang letaknya bersesuaian, dan
> Selisih A-B adalah matriks yang diperoleh dengan mengurangkan elemen-elemen A dengan elemen-elemen B yang letaknya bersesuaian.
c. Perkalian Matriks
Perkalian matriks dibedakan menjadi 2, yaitu perkalian skalar dan perkalian matriks. Mari kita bahas satu persatu.
i. Perkalian Skalar Matriks
Jika k adalah bilangan real dan A=(aij)mxn adalah sebuah matriks maka kA=k(aij)mxn = (kaij)mxn.
Maksudnya bagaimana ?
mari pelajari contoh berikut ini supaya lebih mudah dipahami.
ii. Perkalian Matriks dengan Matriks
Misalkan A berordo pxq dan B berordo mxn
Syarat : A X B haruslah q = m , hasil perkalian AB , berordo pxn
(Jumlah baris pada matriks pertama = jumlah kolom pada matriks ke 2)
maka
Contoh :
Misalkan diketahui matriks A dan B seperti di bawah ini. Maka nilai A.B = ....
